De acuerdo con la OMS el año 2016, hubo cerca de 1.35 millones de muertes por accidentes de tránsito y es la primera causa de muerte entre niños y jóvenes de entre 5 a 29 años y algo importante, la tasa de muertes por accidentes de 3 veces más alto en los países de bajos ingresos comparado con los países de altos ingresos [1]
Dentro de los accidentes de tránsito, aquellos que se dan en las carreteras siempre son un tema crítico, ya que los accidentes en las carreteras causan impactos mucho más graves en los conductores y pasajeros, asimismo se puede indicar que, las colisiones delanteras son una gran parte de los accidentes de carretera, y, además, que la mayoría de ellos ocurren debido a la negligencia del conductor de no mantener un avance adecuado con su vehículo anterior [2].
En ese sentido, tienen especial relevancia, los accidentes que tienen lugar en las carreteras de Latinoamérica, en particular los del transporte interprovincial de pasajeros en autobuses, por su elevado número. Si tomamos un caso más específico, de acuerdo con Corrales, los accidentes en el transporte interprovincial de pasajeros en el Perú son muy frecuentes dejando un saldo de muertes muy elevado y de acuerdo con la Policía Nacional del Perú, en los primeros 15 días del mes de enero del año 2018, se han tenido 64 muertos por accidentes de autobuses de transporte interprovincial y un número mayor de heridos, es decir en menos de un mes [3].
Si tomamos datos anuales, el año 2013, de acuerdo con la Comunidad Andina, en el Perú se produjeron 3110 muertos por accidentes de tránsito, de los cuales, 290 muertes se dieron en autobuses de transporte público interprovincial, es decir un porcentaje cercano al 10% de fatalidades por accidentes de tránsito que involucran autobuses, en relación al total de fatalidades por accidentes de tránsito [4]. Este valor está muy por encima de los valores proporcionados por la OMS de países de la región que oscila en 6% [5].
Ahora bien, existen múltiples causas técnicas vinculadas a los accidentes en autobuses como las condiciones y edad de las unidades de transporte, el estado de las carreteras, el conductor, la mala señalización de las carreteras, los trayectos largos, la geometría de las carreteras, la conducción nocturna y otros [6], [7], [8], [9], [10], pero también se puede afirmar que, el desempeño de la seguridad de las empresas de transporte público interprovincial, está determinado tanto por factores del medio ambiente como de organización. Los factores organizativos, incluyen tamaño de la empresa, la edad de la flota, tamaño de la flota operativa, kilometraje, tipo de carga, características del conductor, especificaciones del vehículo, factores de gestión en general y el cumplimiento de las normas de seguridad. Los factores organizacionales con efectos más significativos sobre la seguridad en las empresas de transporte fueron la antigüedad de los autobuses, el capital de la empresa de autobuses y el número medio de infracciones de tráfico de los conductores [11].
Una posible vía para identificar de mejor manera los factores relacionados con los accidentes es utilizar los datos retrospectivos disponibles, como los registros de accidentes de tráfico (TAR). Los TAR suelen contener información relacionada no solo con la gravedad del accidente, sino también con factores potencialmente influyentes en los accidentes, como las instalaciones de la carretera, el modo de tráfico, las condiciones climáticas, las características del conductor y las condiciones del vehículo. Se han utilizado varios tipos de análisis multivariados para utilizar dicha información TAR. La forma de análisis más actualizada sería la minería de datos [12]
De esta manera, resulta importante estudiar las causas aplicando análisis multivariado o herramientas estadísticas que ayuden encontrar aquellas que tienen más importancia, para de esa manera reducir los accidentes atacando estas causas, sin embargo, existen otras herramientas que se pueden usar para ayudar a reducir los accidentes de autobuses en carretera.
En ese sentido, también puede ser interesante poder estimar o predecir los accidentes que pueden suceder en una carretera a través de herramientas como los modelos de simulación.
La simulación es usada de forma muy intensa en todos muchos campos como las finanzas, administración y fabricación y a todo nivel, estratégico, táctico y operativo. En la ingeniería industrial en particular, es ampliamente usada en la gestión de operaciones. La simulación es una herramienta muy útil para la toma de decisiones a todo nivel. Las aplicaciones clásicas de la simulación pasan por diseño del sistema, diseño de instalaciones, disposición de planta, diseño del sistema de manejo de materiales, planificación de las operaciones, programación, control en tiempo real, políticas operativas, diseño de la cadena de suministro, gestión de la cadena de suministro, diseño del proceso, gestión del inventario, gestión del mantenimiento, compras, diseño del producto, ergonomía, gestión del conocimiento, entre otros [13]
En el caso del transporte existen muchos simuladores de tráfico o de red como SUMO, VISSIM, CORSIM, NS-2, NCTUns, JiST, TraNS, STRAW y otros, pero aplicados al trasporte urbano, por ejemplo, en la sincronización de semáforos, identificación de paradas de autobuses, pero no se encuentran muchos simuladores de accidentes y por tanto de accidentes en carretera [2].
En este paper se plantea una propuesta de un modelo de simulación discreto de accidentes en una carretera, para lo cual se define un modelo discreto de simulación, se identifican los factores críticos a considerar en la simulación como variables de entrada y se definen los elementos de salida del simulador. Incluye, la definición del modelo básico de simulación a emplear, supuestos y características del modelo y escenarios de simulación a partir de dos de los factores clave que se han identificado, para lo cual ha sido necesario procesar la data histórica de cinco años de accidentes en carretera, centrándonos en accidentes de unidades de transporte público pesado de pasajeros.
El presente estudio se realizó por medio de tres fases y las herramientas a usarse dependerán de la fase de la investigación.
En la primera fase se recopila la información pertinente de los accidentes a partir de información de la Policía Nacional del Perú y de la Superintendencia de Transporte Terrestre de Carga, Pasajeros y Mercancías (SUTRAN), de 7 años consecutivos, considerando la mayor cantidad de campos de interés que se pueda tener.
La segunda fase: Se procesan los datos y se realiza un análisis de la información a fin de determinar las vías con mayores accidentes. Una vez identificada la vía donde ocurrieron la mayor cantidad de accidentes, se evalúa con más detalle ésta, obteniendo los tramos de esta vía, que tienen la más alta frecuencia de accidentes. Luego, en estos tramos, se analiza la variable: tiempo entre dos accidentes consecutivos, obteniéndose una distribución que se ajuste a los datos. De esta manera sólo se consideran dos factores para el estudio, el tiempo entre accidentes y la ubicación física de los mismos.
La tercera fase: Se usa la distribución obtenida en la primera fase para simular la ocurrencia de los accidentes. Se usa un modelo de simulación que permite simular el número de accidentes por semana, adicionalmente se desarrolla una simulación de muertos y heridos por accidente.
El modelo de simulación se basa en la información obtenida en el análisis de datos. Se usa un periodo de una semana (7 días), donde se simula la variable de número de accidentes en el tramo de carretera, que siguen una distribución de Poisson obtenida a partir de la distribución exponencial anterior [14] y [15].
Sea, T: tiempo entre accidentes en el tramo de carretera, que sabemos se distribuye exponencialmente T ~ Exp(α), donde E(T) = x días; luego, se puede tener para un periodo semanal, la tasa de accidentes λ = αt accidentes por semana con t = 7.
Se define la variable X: Número de accidentes semanales en el tramo de carretera de la Panamericana Norte (en el tramo motivo de estudio), que se distribuye en una Poisson, donde X ~ P(λ).
Se usa el método de convolución para generar el número de accidentes por semana, usando el periodo de 7 días para cada réplica. La generación de cada accidente es acumulativa en la semana, mientras el tiempo no exceda los 7 días; es decir se genera tantos accidentes, como puedan ocurrir en la semana. La Figura 1 muestra el diagrama de flujo de cómo se genera el número de accidentes para una semana estándar.
.png)
Figura 1: Diagrama de flujo de simulación de número de accidentes semanales
Finalmente se simula a través de una distribución de Bernoulli, si en el accidente, está involucrado un autobús o no, determinado de esta manera el número esperado de accidentes en el tramo indicado y adicionalmente, los muertos y heridos relacionados.
La información recopilada de la Policía Nacional del Perú y SUTRAN considera todos los accidentes ocurridos en una de las carreteras nacionales del Perú (las más importantes), dentro del período de 2010 a 2016 e incluye los siguientes campos: Año, mes, día, hora, día de la semana, modalidad del accidente, zona, lugar, km, empresas de transporte (si fuera el caso), cantidad de vehículos involucrados, tipos de vehículos involucrados, fallecidos y heridos. Una vez recopilada la información se procedió a desarrollar las siguientes dos fases del estudio.
En los siguientes tres acápites se presentan las tablas y gráficos, que describen la información relevante para el presente estudio y que, de acuerdo con el marco metodológico, corresponde a la segunda fase de estudio.
Figura2: Accidentes por carretera 2010-2016
Siniestrados por carretera
El análisis de siniestralidad por carretera, nos muestra que la carretera Panamericana Norte es la que muestra el mayor índice de accidentes, para los datos recolectados entre el período de 7 años analizados hasta el año 2016, seguida por la carretera Panamericana Sur. En la Figura 2, se presenta el resultado, de este modo, queda definida la carretera que se debe evaluar, para la simulación.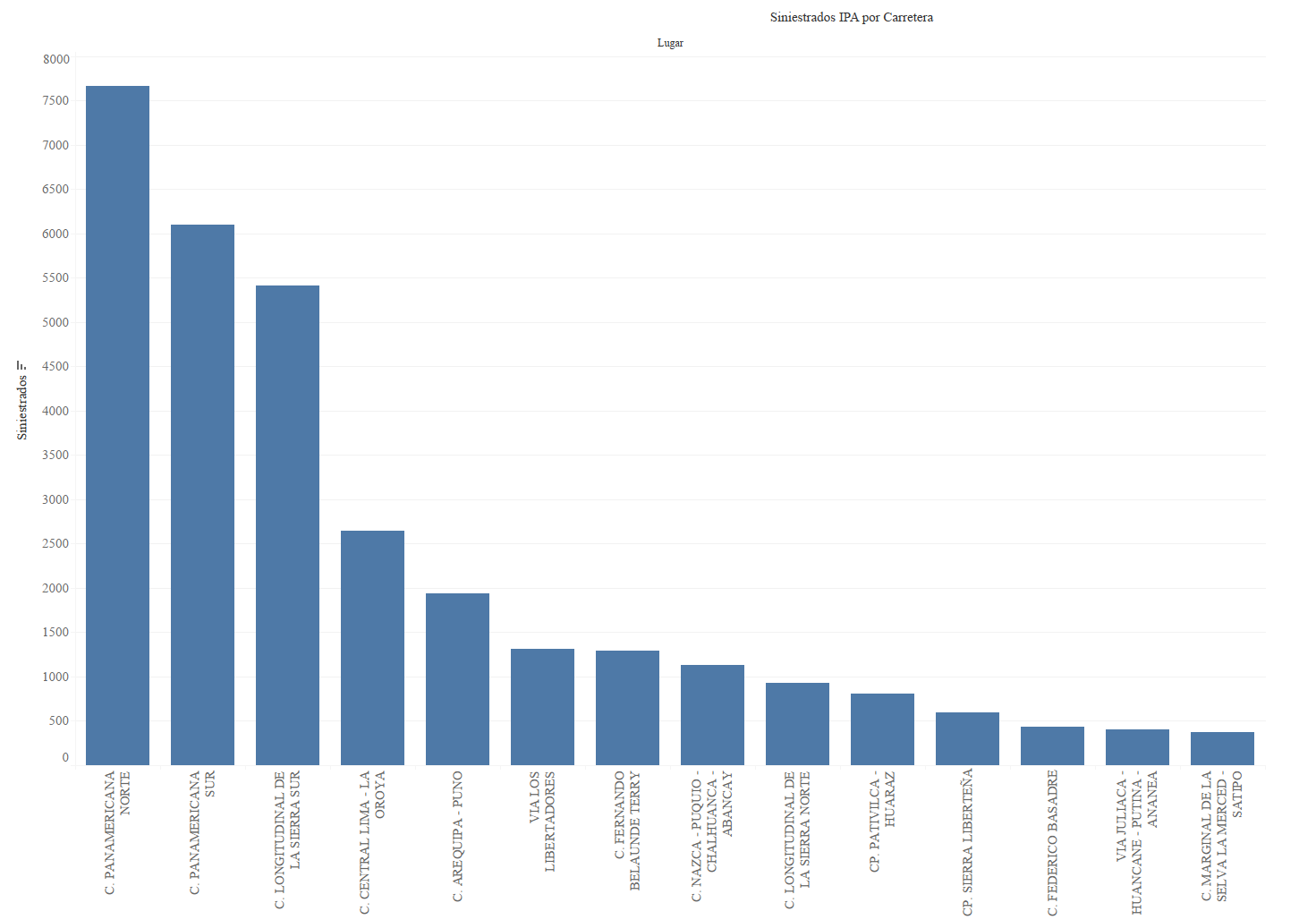
Figura2: Accidentes por carretera 2010-2016
Siniestrados en la carretera Panamericana Norte
Usando nuevamente la información procesada, se analizan los 1250 Km de la carretera Panamericana Norte, para evaluar cuál de los tramos tienen mayor frecuencia de accidentes, obteniéndose que los primeros 200 kilómetros son donde se generan alrededor del 40% de accidentes de esta vía. El histograma de la figura 3, muestra en detalle la información del número de accidentes por rangos de kilómetros.
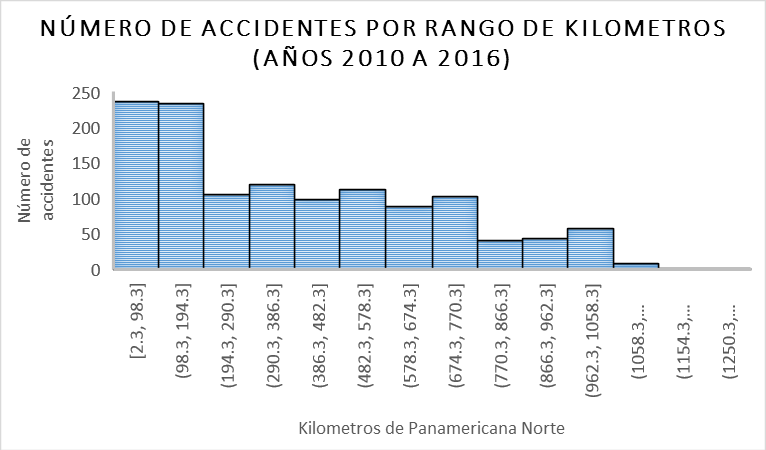
Figura 3: Número de accidentes en carretera Panamericana Norte en los años 2010-2016
Se trabaja en forma más precisa con la información del rango de kilómetros entre el KM00 a KM200, obteniéndose la gráfica de frecuencia de accidentes, mostrada en la Figura 4.
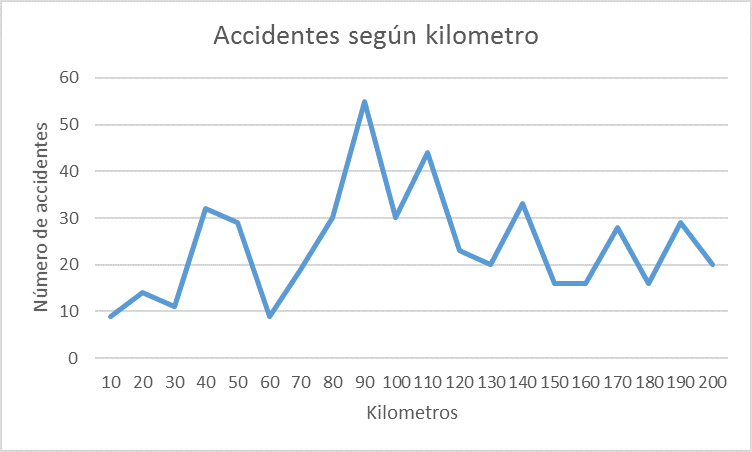
Figura 4: Número de accidentes en carretera Panamericana Norte (KM00-KM200)
En la Tabla 1 se presenta la frecuencia de accidentes por intervalo, analizando intervalos de 10 kilómetros cada uno, observándose que el tramo del KM80 al KM90 es el de mayor incidencia.
Tabla1: Frecuencia de accidentes por intervalos para los primeros 200 kilómetros de la carretera Panamericana Norte
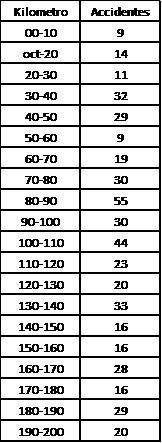
Análisis de tiempos entre accidentes en la carretera Panamericana Norte
En este punto, se analiza la variable tiempo entre accidentes, en la carretera Panamericana Norte, entre los kilómetros KM00 y KM200, como ya se determinó previamente, obteniéndose que los datos se ajustan a una distribución exponencial de media 5.08 días, es decir que los accidentes ocurren en este tramo de carretera cada 5 días en promedio. La Figura 5, muestra las estadísticas de los datos que sustentan la información
.png)
Figura 5: Distribución exponencial para el tiempo entre accidentes
Resultados de la simulación
Como parte de la tercera fase del estudio, se presenta ahora los resultados del modelo básico de simulación desarrollado, para lo cual se han considerado dos factores, el kilómetro, ubicación física, y el tiempo entre accidentes.
Sea, T: tiempo entre accidentes en el tramo de carretera, que sabemos se distribuye exponencialmente T ~ Exp(α = 0.1967), donde E(T) = 5.08 días; luego, se puede tener para un periodo semanal, la tasa de accidentes λ = αt = 0.1967*7 = 1.377 accidentes por semana.
Se define la variable X: Número de accidentes semanales en el tramo de carretera de la Panamericana Norte (KM00 a KM200), que se distribuye en una Poisson, donde X ~ P(λ = 1.377).
Como se indicó en la metodología, se usa el método de convolución para generar el número de accidentes por semana, usando el periodo de 7 días para cada réplica. La generación de cada accidente es acumulativa en la semana, mientras el tiempo no exceda los 7 días; es decir se genera tantos accidentes, como puedan ocurrir en la semana.
Los resultados obtenidos se simularon para 250 réplicas, es decir se simularon 250 semanas independientes, teniendo como resultados los mostrados en la Tabla 2, donde 62 semanas no ocurrió accidente alguno, 88 semanas ocurrieron un solo accidente, 61 semanas ocurrieron dos accidentes, 28 semanas ocurrieron tres accidentes y 11 semanas ocurrieron cuatro accidentes. Esto nos brinda un total de 338 accidentes en 250 semanas de simulación, obteniéndose un promedio de 1.3520 accidentes por semana
Tabla 2: Accidentes por semana
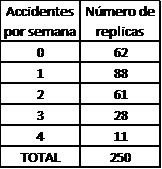
Además, se simuló el número de muertos y heridos para cada accidente, de los 338 accidentes obtenidos en las 250 réplicas, 109 presentaron fallecidos (32%) y 273 presentan heridos (80%); 83 presentan fallecidos y heridos (25%). El número de heridos es de 1203 y el número de fallecidos es 148, esto representa 3.67 heridos y 0.435 fallecidos en promedio.
En la Figura 6 se muestra el detalle de los resultados de la simulación para algunas de las 250 réplicas, que podemos considerar como semanas.
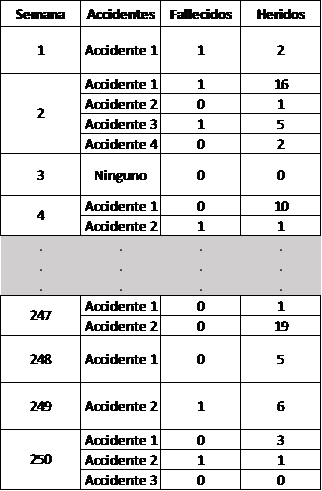
Figura 6: Accidentes por semana con fallecidos y heridos
A partir de los resultados de la simulación se pueden determinar diferentes datos de interes. Algunos de esos datos se presentan en la Tabla 3.
Tabla 3: Resultados de la simulación en promedio por semana
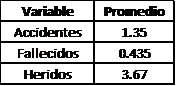
Si analizamos solamente los buses, los cuales representan el 27% de los accidentes en el tramo de la carretera Panamericana Norte, como se presenta en la Tabla 4, tenemos que estos números de reducen.
Tabla 4: Porcentaje de accidentes por tipo de vehículo
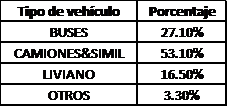
Teniendo en cuenta la particularidad de este ajuste y considerando la situación: autobús tiene accidente, autobús no tiene accidente, podemos usar distribución de Bernoulli para asociar a la simulación de accidente, si está o no involucrado un autobús de pasajeros, obteniendo el resultado mostrado en la Tabla 5, en relación a los accidentes. Para el caso de muertos y heridos no se puede seguir este proceso, pues entran a tallar otras variables como la cantidad de ocupantes de los vehículos, sin embargo, se puede obtener que el número de accidentes estimado de 87 accidentes en las 250 réplicas, que si se consideran 250 semanas nos dan un estimado de un accidente cada tres semanas.
Tabla 5: Número y porcentaje de accidentes de autobuses
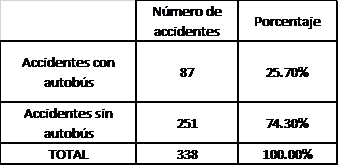
Considerando dos factores vinculados a los accidentes, tiempo entre ellos y ubicación física (km), se puede desarrollar un modelo básico de simulación del número de accidentes en un tramo de carretera, que puede servir de base para simulaciones más complejas, usando más factores y tramos más largos.
El modelo de simulación permite simular el número de accidentes en un tramo de carretera, considerando que el tiempo entre accidentes tiene una distribución exponencial.
El modelo de simulación permite simular el número de accidentes de autobuses, en un tramo de carretera, a partir de las mismas consideraciones anteriores, incluyendo un paso adicional de considerar una distribución de Bernoulli para asociar esta simulación a la anterior.
De esta misma manera se puede simular la cantidad de accidentes por tipo de vehículo, es decir por camiones, camionetas, automóviles, datos que se tienen en la información procesada.
Este modelo podría permitir estimar la cantidad de muertos y heridos, que podría haber en un tramo de carretera, de no tomar medidas para reducir los accidentes.
[1] World Health Organization (2018). Global status report on road safety 2018. Obtenible en
https://www.who.int/violence_injury_prevention/road_safety_status/2018/en/
[2] Young, C.P., Chang, B.R., Chen, S.Y., Li‐Chang Wang, S.Y. (2008). A highway traffic simulator with dedicated short range communications based cooperative collision prediction and warning mechanism. Proceedings of the IEEE Intelligent Vehicles Symposium, Niagara Falls, ON, September 2008; 114– 119
[3]Corrales, C., Rubio, J.C., Atoche, W. (2018). Determinación de empresas con alta y recurrente siniestralidad en el transporte interprovincial peruano. Proceedings of 16 th LACCEI International Multi-Conference for Engineering, Education, and Technology: “Innovation in Education and Inclusion”, Lima, Peru
[4]Comunidad Andina (2014). Accidentes de tránsito en la comunidad andina. Obtenible en http://estadisticas.comunidadandina.org/eportal/contenidos/2437_8.pdf
[5] Organización Mundial de la Salud (2013). Informe sobre la situación mundial de la seguridad. Obtenible en http://www.who.int/violence_injury_prevention/road_safety_status/2013/report/es/
[6] Kaplan, S., Prato, C. (2012). Risk factors associated with bus accident severity in the United States: a generalized ordered logit model. Journal of safety research, 43(3), 171-80.
[7] Zegeer, C., Huang, H., Stutts, J., Rodgman, E., Hummer, E. (1995). Commercial bus accident characteristics and roadway treatments. Transportation Research Record, 1467, 14–22.
[8] Chimbaa, D., Sandob, T., Kwigizilec, V.. (2010). Effect of bus size and operation to crash occurrences. Accident Analysis and Prevention, 42, 2063–2067.
[9] Stevenson, M, Sharwood, L., KeiElkington, J., Meuleners, L, Ivers, R., Grunstein, R., Williamson, A, Haworth, N., Norton, R.. (2010). The Heavy Vehicle Study: a case-control study investigating risk factors for crash in long distance heavy vehicle drivers in Australia. Public Health, 10,162.
[10] Chu, H. (2014). Assessing factors causing severe injuries in crashes of high-deck busesin long-distance driving on freeways. Accident Analysis and Prevention, 62, 130– 136.
[11] Chang, H., Yeh, C.. (2005). Factors affecting the safety performance of bus companies—The experience of Taiwan bus deregulation. Safety Science, 43, 323–344
[12] Sohn, S.Y., Shin, H. (2001). Pattern recognition for road traffic accident severity in Korea. Ergonomics, 2001, Vol. 44, No. 1, 107-117
[13] Polenghi, A. Fumagalli, L., Roda, I. (2018). Role of simulation in industrial engineering: focus on manufacturing systems. IFAC PapersOnLine, 51-11 (2018) 496–501
[14] Banks, J. (2010) Discrete-event system simulation, Upper Saddle River. Montreal: Prentice Hall, c2010.
[15] Law, A. (2015). Simulation modeling and analysis. New York : McGraw-Hill Education,